堆

堆(heap)是一种满足特定条件的完全二叉树，主要可分为两种类型：

小顶堆(min heap)：任意节点的值小于或等于其子节点的值。
大顶堆(max heap)：任意节点的值大于或等于其子节点的值。

heap

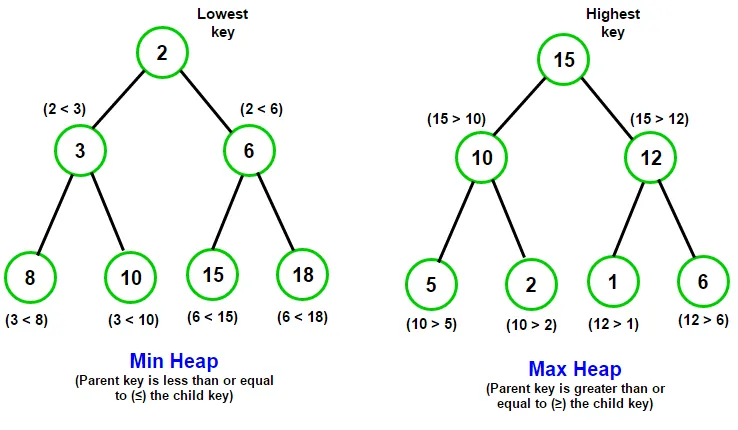
堆作为完全二叉树的一个特例，具有以下特性。

最底层节点靠左填充，其他层的节点都被填满。
我们将二叉树的根节点称为“堆顶”，将底层最靠右的节点称为“堆底”。
对于大顶堆（小顶堆），堆顶元素（根节点）的值是最大（最小）的。

常用操作

堆的常用操作见下表：

方法名	描述	时间复杂度
`push()`	元素入堆	$O(\log n)$
`pop()`	堆顶元素出堆	$O(\log n)$
`peek()`	访问堆顶元素（对于大 / 小顶堆分别为最大 / 小值）	$O(1)$
`size()`	获取堆的元素数量	$O(1)$
`isEmpty()`	判断堆是否为空	$O(1)$

我们来看一个 max heap 的例子：

// Go 语言中可以通过实现 heap.Interface 来构建整数大顶堆
// 实现 heap.Interface 需要同时实现 sort.Interface
type intHeap []any
 
// Push heap.Interface 的方法，实现推入元素到堆
func (h *intHeap) Push(x any) {
    // Push 和 Pop 使用 pointer receiver 作为参数
    // 因为它们不仅会对切片的内容进行调整，还会修改切片的长度。
    *h = append(*h, x.(int))
}
 
// Pop heap.Interface 的方法，实现弹出堆顶元素
func (h *intHeap) Pop() any {
    // 待出堆元素存放在最后
    last := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return last
}
 
// Len sort.Interface 的方法
func (h *intHeap) Len() int {
    return len(*h)
}
 
// Less sort.Interface 的方法
func (h *intHeap) Less(i, j int) bool {
    // 如果实现小顶堆，则需要调整为小于号
    return (*h)[i].(int) > (*h)[j].(int)
}
 
// Swap sort.Interface 的方法
func (h *intHeap) Swap(i, j int) {
    (*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}
 
// Top 获取堆顶元素
func (h *intHeap) Top() any {
    return (*h)[0]
}
 
/* Driver Code */
func TestHeap(t *testing.T) {
    /* 初始化堆 */
    // 初始化大顶堆
    maxHeap := &intHeap{}
    heap.Init(maxHeap)
    /* 元素入堆 */
    // 调用 heap.Interface 的方法，来添加元素
    heap.Push(maxHeap, 1)
    heap.Push(maxHeap, 3)
    heap.Push(maxHeap, 2)
    heap.Push(maxHeap, 4)
    heap.Push(maxHeap, 5)
 
    /* 获取堆顶元素 */
    top := maxHeap.Top()
    fmt.Printf("堆顶元素为 %d\n", top)
 
    /* 堆顶元素出堆 */
    // 调用 heap.Interface 的方法，来移除元素
    heap.Pop(maxHeap) // 5
    heap.Pop(maxHeap) // 4
    heap.Pop(maxHeap) // 3
    heap.Pop(maxHeap) // 2
    heap.Pop(maxHeap) // 1
 
    /* 获取堆大小 */
    size := len(*maxHeap)
    fmt.Printf("堆元素数量为 %d\n", size)
 
    /* 判断堆是否为空 */
    isEmpty := len(*maxHeap) == 0
    fmt.Printf("堆是否为空 %t\n", isEmpty)
}

堆的存储与表示

完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树，因此我们将采用数组来存储堆。

当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。

给定索引 i，其左子节点的索引为 2i+1，右子节点的索引为 2i+2，父节点的索引为(i-1)/2（向下整除）。当索引越界时，表示空节点或节点不存在。

可以将索引映射公式封装成函数，方便后续使用：

/* 获取左子节点的索引 */
func (h *maxHeap) left(i int) int {
    return 2*i + 1
}
 
/* 获取右子节点的索引 */
func (h *maxHeap) right(i int) int {
    return 2*i + 2
}
 
/* 获取父节点的索引 */
func (h *maxHeap) parent(i int) int {
    // 向下整除
    return (i - 1) / 2
}

访问堆顶元素

堆顶元素即为二叉树的根节点，也就是列表的首个元素：

/* 访问堆顶元素 */
func (h *maxHeap) peek() any {
    return h.data[0]
}

元素入堆

给定元素 val ，我们首先将其添加到堆底。添加之后，由于 val 可能大于堆中其他元素，堆的成立条件可能已被破坏，因此需要修复从插入节点到根节点的路径上的各个节点，这个操作被称为堆化 heapify。

考虑从入堆节点开始，从底至顶执行堆化。我们比较插入节点与其父节点的值，如果插入节点更大，则将它们交换。然后继续执行此操作，从底至顶修复堆中的各个节点，直至越过根节点或遇到无须交换的节点时结束。

代码如下所示：

/* 元素入堆 */
func (h *maxHeap) push(val any) {
    // 添加节点
    h.data = append(h.data, val)
    // 从底至顶堆化
    h.siftUp(len(h.data) - 1)
}
 
/* 从节点 i 开始，从底至顶堆化 */
func (h *maxHeap) siftUp(i int) {
    for true {
        // 获取节点 i 的父节点
        p := h.parent(i)
        // 当“越过根节点”或“节点无须修复”时，结束堆化
        if p < 0 || h.data[i].(int) <= h.data[p].(int) {
            break
        }
        // 交换两节点
        h.swap(i, p)
        // 循环向上堆化
        i = p
    }
}

堆顶元素出堆

堆顶元素是二叉树的根节点，即列表首元素。为了尽量减少元素索引的变动，我们采用以下操作步骤。

交换堆顶元素与堆底元素（交换根节点与最右叶节点）
交换完成后，将堆底从列表中删除
从根节点开始，从顶至底执行堆化操作

“从顶至底堆化”的操作方向与“从底至顶堆化”相反，我们将根节点的值与其两个子节点的值进行比较，将最大的子节点与根节点交换。然后循环执行此操作，直到越过叶节点或遇到无须交换的节点时结束。

与元素入堆操作相似，堆顶元素出堆操作的时间复杂度也为 O(logn)，代码如下：

/* 元素出堆 */
func (h *maxHeap) pop() any {
    // 判空处理
    if h.isEmpty() {
        fmt.Println("error")
        return nil
    }
    // 交换根节点与最右叶节点（交换首元素与尾元素）
    h.swap(0, h.size()-1)
    // 删除节点
    val := h.data[len(h.data)-1]
    h.data = h.data[:len(h.data)-1]
    // 从顶至底堆化
    h.siftDown(0)
 
    // 返回堆顶元素
    return val
}
 
/* 从节点 i 开始，从顶至底堆化 */
func (h *maxHeap) siftDown(i int) {
    for true {
        // 判断节点 i, l, r 中值最大的节点，记为 max
        l, r, max := h.left(i), h.right(i), i
        if l < h.size() && h.data[l].(int) > h.data[max].(int) {
            max = l
        }
        if r < h.size() && h.data[r].(int) > h.data[max].(int) {
            max = r
        }
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if max == i {
            break
        }
        // 交换两节点
        h.swap(i, max)
        // 循环向下堆化
        i = max
    }
}

树(tree)图(graph)